Falciparum malaria transmission in Masvingo district, Zimbabwe: a mathematical model with varying human and mosquito populations
Taremba Chirigo1, Esther Chigidi2, Herbert Tafadzwa Kazonda3
1Department of Environmental Health, National University of Science and Technology, Bulawayo, Zimbabwe, 2Department of Mathematics, Midlands State University, Gweru, Zimbabwe, 3Department of Environmental Health: Masvingo Polytechnic
&Corresponding author:Taremba Chirigo, Department of Environmental Health, National University of Science and Technology, Bulawayo, Zimbabwe, Email: [email protected], Tel: +263772316872
Received: 18 Dec 2024 – Accepted: 03 Mar 2025 – Published: 31 Mar 2025
Domain: Malaria Elimination, Infectious Disease Epidemiology
Keywords: Deterministic, falciparum malaria, disease-free equilibrium, malaria elimination, modelling, SEIR, SEI
©Taremba Chirigo et al Journal of Interventional Epidemiology and Public Health (ISSN: 2664-2824). This is an Open Access article distributed under the terms of the Creative Commons Attribution International 4.0 License (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Cite this article: Taremba Chirigo et al Falciparum malaria transmission in Masvingo district, Zimbabwe: a mathematical model with varying human and mosquito populations. Journal of Interventional Epidemiology and Public Health. 2025;8:14. https://doi.org/10.37432/jieph-d-24-02054
Abstract
Introduction: Malaria significantly and disproportionately affects people`s quality of life especially the underprivileged and vulnerable. It poses a serious public health threat despite prevention and control efforts. Masvingo district is not spared, hence, the need to develop a falciparum malaria model and identify the existence of the disease-free equilibrium, analyze its stability, and simulate the model, in the wake of the World Health Organisation Global Malaria Target on local elimination.
Methods: Deterministic, ordinary differential equation-based SEIR and SEI compartmentalization were used for dynamic human and mosquito populations, respectively. Fewer humans were infected at any given moment due to intervention efforts and there was a lower probability of transmission from a recovered compared to an infected human. The district of Masvingo was purposively chosen, and DHIS2 malaria data from January 2015 through December 2020 was used.
Results: Following parameter estimation in Microsoft Excel 2019 the disease-free equilibrium point was shown to exist with R0hv<1 indicating that it is locally asymptotically stable. It was noted that the dynamics of malaria transmission was variable, while the incidence was generally declining.
Conclusions: A falciparum malaria model was developed with dynamic human and mosquito populations incorporating recruitment rates, temporary immunity and transmission from recovered humans. The Disease-Free Equilibrium point exists and was shown to be locally asymptotically stable, hence disease will die out suggesting the district is on track to malaria elimination target. To sustain this trajectory a multi-faceted approach is required, including promoting behavior change communication, accessible rapid diagnostic tests and foster collaborations.
Introduction
Malaria continues to pose a significant worldwide threat to livelihoods and public health, especially in low-to-middle-income nations. It is ranked among the top five infectious disease-related causes of death worldwide, along with respiratory infections, HIV/AIDS, diarrheal illnesses, and tuberculosis, despite decades of interventions [1] Osman M, Adu I, Yang C. A Simple SEIR Mathematical Model of Malaria Transmission. ARJOM [Internet]. 2017 Jan 10 [cited 2025 Mar 12];7(3):1–22. Available from: https://journalarjom.com/index.php/ARJOM/article/view/66 https://doi.org/10.9734/ARJOM/2017/37471 . The global estimate of malaria cases in 2023 was at around 263 million associated with an incidence of 60.4 cases per 1000 population at risk, an increase from 58.6 cases per 1000 population at risk in 2022 [2] World Health Organization. World Malaria Report 2024: addressing inequity in the global malaria response [Internet]. Geneva (Switzerland): World H ealth Organization; 2024 Dec 11[cited 2025 Mar 12]; 293 p. Available from: https://www.who.int/teams/global-malaria-programme/reports/world-malaria-report-2024 Download 9789240104440-eng.pdf . In 2020, the World Health Organisation (WHO) estimated that 3.5 billion people were at malaria risk in 87 endemic countries [3] World Health Organization. Global Technical Strategy for Malaria 2016–2030: 2021 Update [Internet]. Geneva (Switzerland): World Health Organization; 2021[cited 2025 Mar 12]; 30 p. Available from: https://iris.who.int/bitstream/handle/10665/342995/9789240031357-eng.pdf Download 9789240031357-eng.pdf . Over the years, there has been success in lowering death rates; but, the disease burden is still huge and is steadily increasing in many areas, most notably the WHO African Region as well as the WHO Eastern Mediterranean Region [4] World Health Organization. Regional data & trends briefing kit: World malaria report 2024. Geneva (Swotzerland): World Health Organization; 2024 Dec 11[cited 2025 Mar 15]. 13 p. Available from: https://cdn.who.int/media/docs/default-source/malaria/world-malaria-reports/world-malaria-report-2024-regional-briefing-kit-eng.pdf?sfvrsn=bceac4ae_9&download=true Download world-malaria-report-2024-regional-briefing-kit-eng.pdf . Poor and marginalized people are frequently the most affected, having little access to medical care and preventative measures [1] Osman M, Adu I, Yang C. A Simple SEIR Mathematical Model of Malaria Transmission. ARJOM [Internet]. 2017 Jan 10 [cited 2025 Mar 12];7(3):1–22. Available from: https://journalarjom.com/index.php/ARJOM/article/view/66 https://doi.org/10.9734/ARJOM/2017/37471 , [2] World Health Organization. World Malaria Report 2024: addressing inequity in the global malaria response [Internet]. Geneva (Switzerland): World Health Organization; 2024 Dec 11[cited 2025 Mar 12]; 293 p. Available from: https://www.who.int/teams/global-malaria-programme/reports/world-malaria-report-2024 Download 9789240104440-eng.pdf , [3] World Health Organization. Global Technical Strategy for Malaria 2016–2030: 2021 Update [Internet]. Geneva (Switzerland): World Health Organization; 2021[cited 2025 Mar 12]; 30 p. Available from: https://iris.who.int/bitstream/handle/10665/342995/9789240031357-eng.pdf Download 9789240031357-eng.pdf , [4] World Health Organization. Regional data & trends briefing kit: World malaria report 2024. Geneva (Swotzerland): World Health Organization; 2024 Dec 11[cited 2025 Mar 15]. 13 p. Available from: https://cdn.who.int/media/docs/default-source/malaria/world-malaria-reports/world-malaria-report-2024-regional-briefing-kit-eng.pdf?sfvrsn=bceac4ae_9&download=true Download world-malaria-report-2024-regional-briefing-kit-eng.pdf , . The WHO Global Technical Strategy for Malaria highlights the need for better coordinated and strengthened efforts to battle the illness, as the existing global response to malaria is falling short of the targets established for 2025 and 2030 [3] World Health Organization. Global Technical Strategy for Malaria 2016–2030: 2021 Update [Internet]. Geneva (Switzerland): World Health Organization; 2021[cited 2025 Mar 12]; 30 p. Available from: https://iris.who.int/bitstream/handle/10665/342995/9789240031357-eng.pdf Download 9789240031357-eng.pdf Controlling the spread of malaria has been a major focus of effort since ancient times, with the ultimate goal being to lessen local transmission and finally eradicate the illness. Reducing morbidity and mortality by 50% was the main goal of malaria control initiatives between 2000 and 2015 [5] Rowe AK. Assessing the Health Impact of Malaria Control Interventions in the MDG/Sustainable Development Goal Era: A New Generation of Impact Evaluations. Am J Trop Med Hyg [Internet]. 2017 Sep 27 [cited 2025 Mar 12];97(3_Suppl):6–8. Available from: https://ajtmh.org/doi/10.4269/ajtmh.17-0509 2017; 97(Suppl 3):6–8. https://doi.org/10.4269/ajtmh.17-0509 . One of the main goals of the Zimbabwe National Health Strategy [6] Ministry of Health & Child Care Republic of Zimbabwe. National Health Strategy 2021 – 2025[Internet]. Harare (Zimbabwe): Ministry of Health & Child Care Republic of Zimbabwe; 2021 [cited 2025 Mar 15]. 103 p. Available from: https://www.scribd.com/document/590031144/National-Health-Strategy-for-Zimbabwe-2021-2025 Download National Health Strategy for Zimbabwe[2021_2025]_085222.pdf was to lower the incidence of malaria from 39 cases per 1,000 people in 2014 to 5 cases per 1,000 people by 2020, and to almost completely eliminate malaria-related deaths by the same year. In spite of these lofty objectives, the national incidence rate of malaria stayed at 29 cases per 1,000 population-at risk (PAR) in 2017, declining to 19 cases per 1,000 PAR in 2018, and then somewhat rising to 22 cases per 1,000 PAR in 2019 [6] Ministry of Health & Child Care Republic of Zimbabwe. National Health Strategy 2021 – 2025[Internet]. Harare (Zimbabwe): Ministry of Health & Child Care Republic of Zimbabwe; 2021 [cited 2025 Mar 15]. 103 p. Available from: https://www.scribd.com/document/590031144/National-Health-Strategy-for-Zimbabwe-2021-2025 Download National Health Strategy for Zimbabwe[2021_2025]_085222.pdf . As part of a larger plan to eradicate malaria, this raises questions about Zimbabwe’s capacity to achieve its current targets of reducing malaria incidence by 75% by 2025 and by 90% by 2030 [2] World Health Organization. World Malaria Report 2024: addressing inequity in the global malaria response [Internet]. Geneva (Switzerland): World Health Organization; 2024 Dec 11[cited 2025 Mar 12]; 293 p. Available from: https://www.who.int/teams/global-malaria-programme/reports/world-malaria-report-2024 Download 9789240104440-eng.pdf , [3] World Health Organization. Global Technical Strategy for Malaria 2016–2030: 2021 Update [Internet]. Geneva (Switzerland): World Health Organization; 2021[cited 2025 Mar 12]; 30 p. Available from: https://iris.who.int/bitstream/handle/10665/342995/9789240031357-eng.pdf Download 9789240031357-eng.pdf .. To accomplish these goals, more effective and long-lasting interventions are required, according to recent studies. The World Health Organization reported that for ten high burden African countries, there was an increase of 3.5 million cases in 2017 over the prior year [7] World Health Organization. World malaria report 2018[Internet]. Geneva (Switzerland): World Health Organization; 2018 [cited 2025 Mar 12]. 165 p. Available from: https://iris.who.int/bitstream/handle/10665/275867/9789241565653-eng.pdf?sequence=1 Download 789241565653-eng.pdf . In the same report, however, Zimbabwe recorded 0.6 million fewer malaria cases in 2018 than in 2017. Despite this decline, Zimbabwe remains a high burden malaria country with about thirty of the sixty-two districts classified as heavy burden malaria districts. For low-burden malaria districts (incidence rate < 5 cases per 1000 PAR) Zimbabwe initiated elimination activities in 20 districts by 2015 and as of 2019 the districts implementing a package of elimination interventions expanded to 29 [8] U.S. President’s Malaria Initiative Zimbabwe Malaria Operational Plan FY 2020 [Internet]. Atlanta (GA): U.S. President’s Malaria Initiative; 2020 [cited 2025 Mar 17]. 133 p. Available from: www.pmi.gov Download ZIMBABWE Malaria Operational Plan FY 2024.pdf . These elimination intervention packages include case management, case investigation and classification, and foci investigation and classification, among others. Three of the low-burden malaria districts (Gutu, Chivi and Masvingo) in Masvingo province are being targeted for malaria elimination. Visual analysis of Masvingo provincial DHIS2 malaria data from 2014 to 2019 identified Masvingo district as a target district for analysis and modelling. In 2018, the district recorded an incidence rate of 2-4 cases per 1000 [8] U.S. President’s Malaria Initiative Zimbabwe Malaria Operational Plan FY 2020 [Internet]. Atlanta (GA): U.S. President’s Malaria Initiative; 2020 [cited 2025 Mar 17]. 133 p. Available from: www.pmi.gov Download ZIMBABWE Malaria Operational Plan FY 2024.pdf . The district started implementing elimination packages in 2018 and is one of the target districts for disease elimination by 2030. Although there has been some reduction in malaria incidence, but with the objective to locally eliminate the disease, the cyclical nature of the incidence pattern remains of major concern. Hence the necessity to mathematically model the falciparum malaria transmission dynamics in variable human and mosquito populations and assess the implications this has on prevention and control of the disease. Several authors have developed mathematical models to understand host-vector interactions, transmission dynamics and control measures for local malaria elimination [9] Ngwa GA, Shu WS. A mathematical model for endemic malaria with variable human and mosquito populations. Mathematical and Computer Modelling [Internet]. 2000 Oct [cited 2025 Mar 12];32(7–8):747–63. Available from: https://linkinghub.elsevier.com/retrieve/pii/S0895717700001692 https://doi.org/10.1016/S0895-7177(00)00169-2 , [10] Walker, P. G. T., Griffin, J. T., Ferguson, N. M., & Ghani, A. C. Estimating the most efficient allocation of interventions to achieve reductions in Plasmodium falciparum malaria burden and transmission in Africa: A modelling study. The Lancet Glob Health [Internet]. 2016 Jul [cited 2025 Mar 12];4(7):e474–e484. Available from: https://www.thelancet.com/journals/langlo/article/PIIS2214-109X(16)30073-0/fulltext https://doi.org/10.1016/S2214-109X(16)30073-0 , [11] Baihaqi, M. A. & Adi-Kusumo, F. Modelling malaria transmission in a population withSEIRp method. Symposium on BioMathematics 2019 ( SYMOMATH 2019) [Internet]. AIP Conf. Proc. 2020; 2264:020002-1 – 020002-12. Bali (Indonesia): AIP Publishing; 2020 Sep 22[cited 2025 Mar 12]; 12 p. Available from: https://pubs.aip.org/aip/acp/article/2264/1/020002/1013132/Modelling-malaria-transmission-in-a-population https://doi.org/10.1063/5.0023508 Download 020002_1_online.pdf . Compartmental SEIR models have often been used to capture such transmission dynamics between humans and mosquitoes incorporating factors such as newborns and loss in immunity among the recovered population [11] Baihaqi, M. A. & Adi-Kusumo, F. Modelling malaria transmission in a population withSEIRp method. Symposium on BioMathematics 2019 ( SYMOMATH 2019) [Internet]. AIP Conf. Proc. 2020; 2264:020002-1 – 020002-12. Bali (Indonesia): AIP Publishing; 2020 Sep 22[cited 2025 Mar 12]; 12 p. Available from: https://pubs.aip.org/aip/acp/article/2264/1/020002/1013132/Modelling-malaria-transmission-in-a-population https://doi.org/10.1063/5.0023508 Download 020002_1_online.pdf . However, they did not consider re-infection of the recovered population. Research has also highlighted the importance of seasonality and heterogeneity [12] Selvaraj, P., Wenger, E. A., & Gerardin, J. Seasonality and heterogeneity of malaria transmission determine success of interventions in high-endemic settings: a modeling study. BMC Infectious Diseases [Internet]. 2018 Aug 22 [cited 2025 Mar 12]; 2018(1):413. Available from: https://bmcinfectdis.biomedcentral.com/articles/10.1186/s12879-018-3319-y https://doi.org/10.1186/s12879-018-3319-y , [13] Griffin JT, Bhatt S, Sinka ME, Gething PW, Lynch M, Patouillard E, Shutes E, Newman RD, Alonso P, Cibulskis RE, Ghani AC. Potential for reduction of burden and local elimination of malaria by reducing Plasmodium falciparum malaria transmission: a mathematical modelling study. The Lancet Infectious Diseases [Internet]. 2016 Apr 19 [cited 2025 Mar 12];16(4):465–72. Available from: https://linkinghub.elsevier.com/retrieve/pii/S1473309915004235 https://doi.org/10.1016/S1473-3099(15)00423-5 ,[14] Andolina C, Rek JC, Briggs J, Okoth J, Musiime A, Ramjith J, Teyssier N, Conrad M, Nankabirwa JI, Lanke K, Rodriguez-Barraquer I, Meerstein-Kessel L, Arinaitwe E, Olwoch P, Rosenthal PJ, Kamya MR, Dorsey G, Greenhouse B, Drakeley C, Staedke SG, Bousema T. Sources of persistent malaria transmission in a setting with effective malaria control in eastern Uganda: a longitudinal, observational cohort study. Lancet Infect Dis [Internet]. 2021 Jun 19 [cited 2025 Mar 12];21(11):1568-1578. Available from: https://linkinghub.elsevier.com/retrieve/pii/S1473309921000724 https://doi.org/10.1016/s1473-3099(21)00072-4 ,[15] Turkson AJ, Addor JA, Ayiah-Mensah F. The Cox Proportional Hazard Regression Model Vis-à-Vis ITN-Factor Impact on Mortality Due to Malaria. OJS [Internet]. 2021 [cited 2025 Mar 12];11(06):931–62. Available from: https://www.scirp.org/journal/doi.aspx?doi=10.4236/ojs.2021.116055 https://doi.org/10.4236/ojs.2021.116055 migration and immunity [16] Smith NR, Trauer JM, Gambhir M, Richards JS, Maude RJ, Keith JM, Flegg JA. Agent-based models of malaria transmission: a systematic review. Malar J [Internet]. 2018 Aug 17[cited 2025 Mar 12];17(1):299. Available from: https://malariajournal.biomedcentral.com/articles/10.1186/s12936-018-2442-y https://doi.org/10.1186/s12936-018-2442-y , optimal times for interventions as well as the need for micro-models to address challenges associated with local variations [17] Egbom SE, Nduka FO, Nzeako SO. Point prevalence mapping of malaria infection in Rivers State, Nigeria. Tanzania J Hlth Res [Internet]. 2022 Sep 27 [cited 2025 Mar 12];23(4):1–11. Available from: https://www.ajol.info/index.php/thrb/article/view/224077 https://doi.org/10.4314/thrb.v23i4.7 . Although not all disease characteristics can be explained by a single model, consideration of these factors enhance a data-driven understanding of disease transmission dynamics and intervention efficacies [18] . Dizon, C., Lysyk, T.J., Couloigner, I. and Cork, S.C. Ecology and Epidemiology of Lyme Disease in Western North America. Zoonotic Diseases [Internet]. 2023 Jan 31;3(1):20-37. Available from: https://www.scienceopen.com/document?vid=a268a629-fd81-43db-997b-cba378686da2 . The current study was aimed to develop a mathematical model for falciparum malaria transmission dynamics in Masvingo district, assessing the implications this has for achieving the WHO 2030 malaria elimination targets. The study also sought to determine the existence and stability of the disease-free equilibrium and to simulate the model using local malaria data. Thus such modeling as this study provides data-driven insights to support and develop tailored policies and strategies that are geographically appropriate and contextually relevant to malaria prevention and control. Thus, it helps track progress on elimination and understand the impact of the current controls on incidence; hence, guide future decisions such as to track progress towards local elimination targets.
Methods
Approach and model formulation
A population-based deterministic approach was used to model the transmission of malaria. The mathematical model consisted of variable human and mosquito populations. The human and mosquito populations were divided into compartments. Infection dynamics in humans were described by ordinary differential equations and used the epidemiological compartment modelling approach as follows: individuals start life being susceptible to falciparum malaria infection (Sh); and these are then exposed at a certain probability to infectious mosquito bites. The exposed (Eh) compartment consists of individuals who are infected but are not capable of infecting others during a latent period. The infectious humans (Ih) give rise to more infected mosquitoes through their interaction with the susceptible mosquitoes. Once treated, individuals recover (Rh) from the disease with partial immunity and after some time they become susceptible again (SEIR). Although the recovered are not at an immediate risk of developing clinical disease, however, they can still infect susceptible mosquitoes but at a lower rate than that of infectious individuals [19].
Infection dynamics in mosquito vectors followed the SEI pattern of compartimentalisation: susceptible mosquitoes (Sv) get infected at a certain probability when they get a blood meal either from infectious humans or recovered humans; then move to exposed compartment (Ev) and finally the infectious compartment (Iv). The recovered class is here omitted for the mosquito population because once infected the mosquito remains so until death.
The adapted SEIR model was based on Ngwa and Shu [9]. The SEIR model of compartmentalization (Figure 1 was chosen because it is more realistic as it includes the latent phase (exposed class) which is not found in SIR or SIS models.
In the Ngwa and Shu model [9], humans follow an SEIR pattern while mosquitoes follow the SEI pattern of compartmentalization. Infectious humans either recover with or without immunity; and those who recover with partial immunity remain infectious while those who recover without immunity return directly to the susceptible compartment. The modeling approach adopted in this research is a modification of the Ngwa and Shu model capturing variable human and mosquito populations, preventive intervention measures such as Long-Lasting Insecticidal Nets (LLINS), immigration, recovery with temporary immunity and disease-induced death in humans. The direct infectious-to-susceptible transfer that the Ngwa and Shu model contains is excluded from the model, because most people show some varying periods of immunity before becoming susceptible again [19]. Interaction between the two populations is as shown in Figure 1.
Description of model parameters
With reference to Figure 1, Table 1 provides descriptions of the parameters used in the malaria model.
Model assumptions
- The populations under study are heterogeneous and varying with time,
- Once infected, mosquitoes remain so until death,
- The force of infection for humans is not proportional to the average density of infectious vector capacity, but a lower proportion is infected at any given exposure due to the presence of preventive interventions such as LLINs;
- The probability of transmitting infection to susceptible mosquitoes by infectious humans is greater than that by partially immune recovered humans,
- A person/ mosquito can die at any stage due to natural causes;
- A person once infected can progress to the recovered class or can die from the disease
- Humans recover with temporary immunity, and so can re-enter the susceptible compartment.
- Mosquito dispersal, or migration from surrounding districts is negligible.
Model equations
In view of the model assumptions above and the schematic diagram in Figure 1, the dynamics of malaria transmission was described by the following model equations: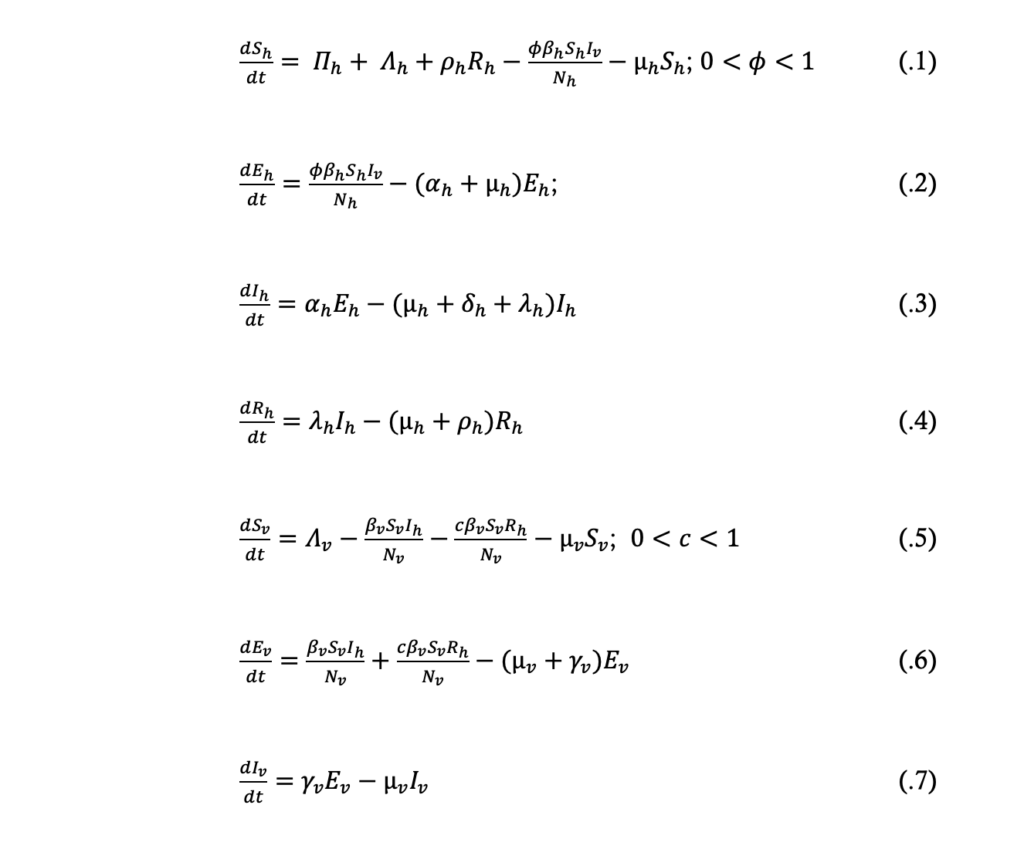
From the model equations (.1) to (.4) the total population size, Nh, at time t is given by:

From the model equations (.5) to (.7) the total population size, Nv, at time t is given by:

Model fitting, validation and parameter estimation
A least-squares estimation method in Microsoft excel 2019 was used to fit the model system (.1) to (.7). Model calibration was done using the full dataset from 2015 – 2020. The dataset for December 2020 – February 2021 was used to assess and strengthen the model’s predictive abilities. Parameter estimation and model simulation were carried out in Microsoft excel 2019.
Results
The disease-free equilibrium point was determined and the local stability of the system was described in terms of the threshold parameter, the basic reproduction number (R0), which was obtained using the next generation matrix method.
Existence of the disease-free equilibrium (DFE) point
The DFE point are steady state solutions where there is no malaria in the human population, and no plasmodium parasites in mosquitoes. Thus the DFE point, given by E0hv (Sh,Eh,Ih,Rh;Sv,Ev,Iv) of the system of differential equations .1 to .7, is obtained by solving the equation

The “infected” classes in the human or mosquito populations are either the exposed or infectious, that is \( E_h, I_h, R_h, E_v, I_v \). So in the absence of disease, at the DFE point of the system (.1) to (.7), it implies \( E_h = I_h = R_h = E_v = I_v = 0 \); \( S_h = \frac{\Pi_h + \Delta_h}{\mu_h} \), and \( S_v = \frac{\Delta_v}{\mu_v} \)
Thus the DFE point \( E_{0hv}(S_h, E_h, I_h, R_h, S_v, E_v, I_v) \) is given by
\( E_{0hv} \left( \frac{\Pi_h + \Delta_h}{\mu_h}, 0, 0, 0; \frac{\Delta_v}{\mu_v}, 0, 0 \right) \).
As such, the positive feasible region of the system for the human population, equations (.1) to (.4) is given by
$$ \{(S_h,E_h,I_h,R_h ): S_h+E_h+I_h+R_h\leq \frac{\Pi_h+\Lambda_h}{\mu_h}, S_h>0,E_h\geq0,I_h\geq0,R_h\geq0\}. $$
The positive feasible region of the model equations (.5) to (.7) for the mosquito population is given by
$$ \{(S_v,E_v,I_v ): S_v+E_v+I_v\leq \frac{\Lambda_v}{\mu_v}, S_v>0,E_v\geq0,I_v\geq0\}. $$
It follows therefore that the DFE point, \( E_{0hv} \left( \frac{\Pi_h+\Lambda_h}{\mu_h} ,0,0,0; \frac{\Lambda_v}{\mu_v} ,0,0 \right) \), of the system of equations (.1) to (.7) is locally asymptotically stable if \( R_{0hv}<1 \) and unstable if \( R_{0hv}>1 \), where
$$ R_{0hv}=\sqrt{R_{0h} R_{0v}}. $$
The square root is as a result of the needed two generations for an infected vector or host to reproduce itself. \( R_{0hv} \) is the basic reproduction number of the system, while \( R_{0h} \) and \( R_{0v} \) are the basic reproduction numbers for human and mosquito populations, respectively.
The basic reproduction number, R0
The basic reproduction number, R0, is defined as the number of secondary infections that one infectious individual generates over the duration of his/ her entire infectious period, assuming that all the individuals in the population are susceptible.
When R0 < 1, each infected individual produces, on average, less than one new infected individual and hence it is expected that the disease will die out. On the other hand, if , each individual produces more than one new infected individual, so it would be expected that the disease will spread through the population. Therefore, the threshold condition for eliminating or eradicating the disease is to reduce the value of to less than one.
We introduce new variables in terms of proportion as follows:

Where
$$ s+e+i+r=1; \quad x+y+z=1; \quad (1.2b) $$
$$ s=(1-e-i-r), \quad \text{and} \quad x=(1-y-z); $$
$$ S_h=sN_h \quad \text{and} \quad S_v=xN_v. $$
Hence
$$ S_h=(1-e-i-r) N_h, \quad \text{and} \quad S_v=(1-y-z) N_v. \quad (1.2c) $$
Now from equations (1.2a), it can be seen that:
$$ N_h \frac{ds}{dt} = \frac{dS_h}{dt} – s \frac{dN_h}{dt} \quad (1.3a) $$
$$ N_h \frac{de}{dt} = \frac{dE_h}{dt} – e \frac{dN_h}{dt} \quad (1.3b) $$
$$ N_h \frac{di}{dt} = \frac{dI_h}{dt} – i \frac{dN_h}{dt} \quad (1.3c) $$
$$ N_h \frac{dr}{dt} = \frac{dR_h}{dt} – r \frac{dN_h}{dt} \quad (1.3d) $$
$$ N_v \frac{dx}{dt} = \frac{dS_v}{dt} – x \frac{dN_v}{dt} \quad (1.3e) $$
$$ N_v \frac{dy}{dt} = \frac{dE_v}{dt} – y \frac{dN_v}{dt} \quad (1.3f) $$
$$ N_v \frac{dz}{dt} = \frac{dI_v}{dt} – z \frac{dN_v}{dt} \quad (1.3g) $$
Using the relationships of equations (1.2) and (1.3), and re-writing the system equations (.1) to (.7) gives the following equations:
$$ \frac{ds}{dt} = a + b + \rho_h r – \phi \beta_h sz – (a + b – \delta_h i)s \quad (1.4) $$
$$ \frac{de}{dt} = \phi \beta_h sz – (a + b + \alpha_h – \delta_h i)e \quad (1.5) $$
$$ \frac{di}{dt} = \alpha_h e – (a + b + \delta_h + \lambda_h – \delta_h i)i \quad (1.6) $$
$$ \frac{dr}{dt} = \lambda_h i – (a + b + \rho_h – \delta_h i)r \quad (1.7) $$
$$ \frac{dx}{dt} = d – \beta_v xi – c\beta_v xr – dx \quad (1.8) $$
$$ \frac{dy}{dt} = \beta_v xi + c\beta_v xr – (\gamma_v + d)y \quad (1.9) $$
$$ \frac{dz}{dt} = \gamma_v y – dz \quad (1.10) $$
The infected classes of the system (.1) to (.7), and hence system (1.4) to (1.10), are now \( e, i, r, y, \) and \( z \). The next generation matrix method was used to determine the \( R_0 \) of the present model. The \( R_0 \) is taken to be the dominant eigenvalue of the next generation matrix. This is given by the matrix \( FV^{-1} \), where \( F \) represents the rate of appearance of new infections in the compartments and \( V \) represents the transfer of individuals in and out of compartments, and \( E_0 \) is the disease-free equilibrium point. Thus:
$$ F \begin{bmatrix} e \\ i \\ r \\ y \\ z \end{bmatrix} =
\begin{bmatrix} \phi \beta_h sz \\ 0 \\ 0 \\ \beta_v xi + c\beta_v xr \\ 0 \end{bmatrix} $$
$$ F(E_0) = \begin{bmatrix} 0 & 0 & 0 & 0 & \phi\beta_h \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & \beta_v & c\beta_v & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{bmatrix} $$
And
$$ V \begin{bmatrix} e \\ i \\ r \\ y \\ z \end{bmatrix} =
\begin{bmatrix} (a+b+\alpha_h – \delta_h i)e \\ -\alpha_h e + (a+b+\delta_h+\lambda_h – \delta_h i)i \\ -\lambda_h i + (a+b+\rho_h – \delta_h i)r \\ (d+\gamma_v )y \\ -\gamma_v y + dz \end{bmatrix} $$
$$ V(E_0) = \begin{bmatrix} (a+b+\alpha_h) & 0 & 0 & 0 & 0 \\ -\alpha_h & (a+b+\delta_h+\lambda_h) & 0 & 0 & 0 \\ 0 & -\lambda_h & (a+b+\rho_h) & 0 & 0 \\ 0 & 0 & 0 & (d+\gamma_v) & 0 \\ 0 & 0 & 0 & -\gamma_v & d \end{bmatrix} $$
Let
$$ a_{11} = (a+b+\alpha_h), \quad a_{21} = -\alpha_h, \quad a_{22} = (a+b+\delta_h+\lambda_h), \quad a_{32} = -\lambda_h, \quad a_{33} = (a+b+\rho_h), \quad a_{44} = (d+\gamma_v), \quad a_{54} = -\gamma_v, \quad a_{55} = d. $$
Then it implies:
$$ |V| = a_{11} a_{22} a_{33} a_{44} a_{55}. $$
Let \( V \) be a vector \( V \) as a matrix of its cofactors, it then implies:
$$ V = \begin{bmatrix} a_{22} a_{33} a_{44} a_{55} & -a_{21} a_{33} a_{44} a_{55} & a_{21} a_{32} a_{44} a_{55} & 0 & 0 \\ 0 & a_{11} a_{33} a_{44} a_{55} & -a_{11} a_{32} a_{44} a_{55} & 0 & 0 \\ 0 & 0 & a_{11} a_{22} a_{44} a_{55} & 0 & 0 \\ 0 & 0 & 0 & -a_{11} a_{22} a_{33} a_{54} & 0 \\ 0 & 0 & 0 & 0 & 0 \end{bmatrix} $$
Then
$$ V^T = \begin{bmatrix} a_{22} a_{33} a_{44} a_{55} & 0 & 0 & 0 & 0 \\ -a_{21} a_{33} a_{44} a_{55} & a_{11} a_{33} a_{44} a_{55} & 0 & 0 & 0 \\ a_{21} a_{32} a_{44} a_{55} & -a_{11} a_{32} a_{44} a_{55} & a_{11} a_{22} a_{44} a_{55} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & -a_{11} a_{22} a_{33} a_{54} & 0 \end{bmatrix} $$
$$ V^{-1} = \frac{1}{|V|} V^T \quad (1.11) $$
$$ = \begin{bmatrix} \frac{1}{a_{11}} & 0 & 0 & 0 & 0 \\ \frac{-a_{21}}{a_{11} a_{22}} & \frac{1}{a_{22}} & 0 & 0 & 0 \\ \frac{a_{21} a_{32}}{a_{11} a_{22} a_{33}} & \frac{-a_{32}}{a_{22} a_{33}} & \frac{1}{a_{33}} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & \frac{-a_{54}}{a_{44} a_{55}} & 0 \end{bmatrix} $$
Therefore, the basic reproduction number \( R_{0hv} \) is thus given by:
$$ R_{0hv} = \sqrt{R_{0h} R_{0v}} $$
Therefore:
$$
R_{0hv} = \sqrt{ \left( \left[ \frac{\alpha_h \beta_v}{(a+b+\alpha_h)(a+b+\delta_h+\lambda_h)} + \frac{c\beta_h \alpha_h \lambda_h}{(a+b+\alpha_h)(a+b+\delta_h+\lambda_h)(a+b+\rho_h)} \right] \cdot \left( \frac{\varphi \beta_h \gamma_v}{d(d+\gamma_v)} \right) \right) }
$$
$$
R_{0hv} = \sqrt{ \frac{\varphi \beta_h \gamma_v \left[ \alpha_h \beta_v (a+b+\rho_h) + c\beta_v \alpha_h \lambda_h \right]}{d(d+\gamma_v)(a+b+\alpha_h)(a+b+\delta_h+\lambda_h)(a+b+\rho_h)} }
$$
$$ R_{0hv} = \sqrt{\frac{\phi \beta_h \gamma_v [\alpha_h \beta_v (a+b+\rho_h) + c\beta_v \alpha_h \lambda_h]}{d(d+\gamma_v)(a+b+\alpha_h)(a+b+\delta_h+\lambda_h)(a+b+\rho_h)}} $$
$$ = 0.096906348 \quad \text{(from Table 4); } R_{0hv} < 1. $$
Malaria transmission is here depicted as resulting from transmission of the plasmodia parasites from infected humans to susceptible mosquitoes and from infected mosquitoes to susceptible humans. The \( R_{0hv} \) here is related to the transmission of disease by infectious humans in the \( I \) compartment, and/or partially immune recovered in the \( R \) compartment to susceptible mosquitoes. Susceptible humans are infected following infectious bites by infected mosquitoes.
Thus, near the DFE (\( E_{0hv} \)) point, each infected human is likely to produce:
$$
\frac{\beta_v \gamma_v}{d(d+\gamma_v)}
$$
new infected mosquitoes, while each infected mosquito is likely to produce:
$$
\frac{\varphi \beta_h \alpha_h (a+b+\rho_h+c\lambda_h)}{(a+b+\alpha_h)(a+b+\delta_h+\lambda_h)(a+b+\rho_h)}
$$
new infected humans during their infectious period.
Stability analysis of the DFE (\( E_{0hv} \)) point
The DFE (\( E_{0hv} \)) point is locally asymptotically stable if \( R_{0hv} < 1 \) and unstable if otherwise. If \( R_{0hv} < 1 \), then the solutions of the equation:
$$
J|E_{0hv} – \lambda I| = 0
$$
are all negative.
Theorem: Considering the disease transmission model given by equations (.1) to (.7) re-written as equations (1.4) to (1.10). If \( E_{0hv} \) is the DFE point of the model, then \( E_{0hv} \) is locally asymptotically stable if the eigenvalues of the matrix (1.12) are all negative.
Proof: The Jacobian of the system (1.4) to (1.10) is obtained as:
$$
J(s,e,i,r;x,y,z) =
\begin{bmatrix}
A & 0 & \delta_h s & \rho_h & 0 & 0 & -\varphi \beta_h s \\
\varphi \beta_h z & B & \delta_h e & 0 & 0 & 0 & \varphi \beta_h s \\
0 & \alpha_h & C & 0 & 0 & 0 & 0 \\
0 & 0 & \lambda_h & D & 0 & 0 & 0 \\
0 & 0 & -\beta_v x & -c\beta_v x & -(\beta_v i + c\beta_v r) – d & 0 & 0 \\
0 & 0 & \beta_v x & c\beta_v x & \beta_v i + c\beta_v r & -(\gamma_v + d) & 0 \\
0 & 0 & 0 & 0 & 0 & \gamma_v & -d
\end{bmatrix}
$$
Where:
$$
A = -\varphi \beta_h z – (a + b – \delta_h i)
$$
$$
B = -( \alpha_h + a + b – \delta_h i)
$$
$$
C = -(a + b – \delta_h i + \delta_h + \lambda_h)
$$
$$
D = -( \rho_h + a + b – \delta_h i)
$$
When the system is evaluated at the DFE point, \( E_{0hv} \), it becomes:
$$
J(E_{0hv}) =
\begin{bmatrix}
-(a+b) & 0 & \delta_h & \rho_h & 0 & 0 & -\varphi \beta_h \\
0 & -( \alpha_h + a + b) & 0 & 0 & 0 & 0 & \varphi \beta_h \\
0 & \alpha_h & -(a+b+\delta_h+\lambda_h) & 0 & 0 & 0 & 0 \\
0 & 0 & \lambda_h & -( \rho_h + a + b) & 0 & 0 & 0 \\
0 & 0 & -\beta_v & -c\beta_v & -d & 0 & 0 \\
0 & 0 & \beta_v & c\beta_v & 0 & -(\gamma_v + d) & 0 \\
0 & 0 & 0 & 0 & 0 & \gamma_v & -d
\end{bmatrix}
$$
Therefore, solving the matrix equation:
$$
J |E_{0hv} – \lambda I| = 0
\quad gives: (1.12)$$
$$
\begin{bmatrix}
-(a+b)-\lambda & 0 & 0 & \rho_h & 0 & 0 & -\varphi \beta_h \\
0 & X & 0 & 0 & 0 & 0 & \varphi \beta_h \\
0 & \alpha_h & Y & 0 & 0 & 0 & 0 \\
0 & 0 & \lambda_h & Z & 0 & 0 & 0 \\
0 & 0 & -\beta_v & -c\beta_v & -d-\lambda & 0 & 0 \\
0 & 0 & \beta_v & c\beta_v & 0 & -(\gamma_v+d)-\lambda & 0 \\
0 & 0 & 0 & 0 & 0 & \gamma_v & -d-\lambda
\end{bmatrix} = 0
\quad (1.13)$$
Where:
$$
X = -(\alpha_h + a + b) – \lambda
$$
$$
Y = -(a+b+\delta_h + \lambda_h) – \lambda
$$
$$
Z = -(\rho_h + a + b) – \lambda
$$
The above equation (1.13) then reduces to:
$$
(-(a+b) – \lambda)\left\{[-(\alpha_h + a + b) – \lambda][- (a + b + \delta_h + \lambda_h) – \lambda][-(\rho_h + a + b) – \lambda](-d – \lambda)[-(\gamma_v + d) – \lambda](-d – \lambda)\right\} – \varphi \beta_h \beta_v \gamma_v \alpha_h (-(a + b) – \lambda)(-c \lambda_h – (a + b) – \lambda) = 0
$$
It then implies:
$$
(-(a+b) – \lambda)(-d – \lambda)\left\{[-(\alpha_h + a + b) – \lambda][- (a + b + \delta_h + \lambda_h) – \lambda][-(\rho_h + a + b) – \lambda][-(\gamma_v + d) – \lambda]\right\} – \varphi \beta_h \beta_v \gamma_v \alpha_h (-c \lambda_h – (\rho_h + a + b) – \lambda) = 0
$$
The solutions to the equation above are:
$$
\lambda_1 = -(a+b), \quad \lambda_2 = -(\alpha_h + a + b), \quad \lambda_3 = -(a + b + \delta_h + \lambda_h), \quad \lambda_4 = -(\rho_h + a + b),
$$
$$
\lambda_5 = -d, \quad \lambda_6 = -(\gamma_v + d), \quad \lambda_7 = -(c \lambda_h + (\rho_h + a + b))
$$
Since the solutions of the model are all negative, it can be concluded that \( E_{0hv} \) is locally asymptotically stable, and hence, \( R_{0hv} < 1 \).
Summary statistics from Masvingo district malaria data
The following table, Table 2, shows the descriptive statistics of monthly confirmed Rapid Diagnostic Test (RDT) positive malaria cases disaggregated by age and sex from 2015 to 2020.
From Table 2, it can be seen that the mean number of confirmed positive malaria cases increases with age.
Table 3 presents summary statistics of the malaria incidence disaggregated by sex and year of occurrence. It can be seen that males generally contribute more malaria cases compared to the female population.
Numerical simulation and projection
Microsoft Excel (2019) was used for parameter estimation and to study the dynamical behavior of the system of equations (1.4) to (1.10). To simplify these model equations, Euler’s method was used. It states that if
The given differential equation is:
$$
\frac{dA}{dt} = -kA + hB^2
$$
And the left-hand side (LHS) is given by:
$$
\text{LHS} = \frac{A_{i+1} – A_i}{\Delta t}
$$
Using the equation above, we can derive:
$$
A_{i+1} = \left( -kA + hB^2 \right) \Delta t + A_i
$$
In the context of malaria transmission in Masvingo district, the parameter values chosen are shown in Table 4[22], and the following initial conditions were selected: and the best model fit, determined by the square of the Pearson’s product moment correlation coefficient ( passing through the data provided is shown in Figure 2. RDNS- positive cases (infected) refers to the individuals who tested malaria positive and notified according to the Rapid Disease Notification System (RDNS). Expected malaria cases were obtained after applying the model to the existing disease data (cases), to see how best it fits the data. The 2-period moving average was obtained by finding the average of two consecutive values which seeks to smooth-out month-to-month fluctuations.
The trend in the incidence of malaria over time is shown. Although there is a general decline in the number of malaria cases, the transmission dynamics is highly fluctuating (Figure 2).
Discussion
An ordinary differential equation-based compartmental model for the transmission of falciparum malaria was formulated for both human and mosquito populations. The basic assumptions underlying the model formulation were stated. The human population was modeled using the SEIR model while the mosquito population was modeled using the SEI model. In formulating the model, humans recovered with partial immunity which waned over time and thus became susceptible again. However, in their recovered state, these humans habour the infectious parasite and thus can infect susceptible mosquitoes but at a lower rate compared to the rate by infectious humans. Model analysis was also done. The existence of a disease free equilibrium (DFE) point was ascertained and was found to be locally asymptotically stable. The basic reproduction number, which is a threshold parameter, was derived and it was shown to be a square-root of the product of the vector reproduction number and the human reproduction number [20] Huo, H., & Qiu, G. Stability of a Mathematical Model of Malaria Transmission with Relapse. Abstract and Applied Analysis [Internet]. 2014[cited 2025 Mar 12]; 2014:1–9. Available from: http://www.hindawi.com/journals/aaa/2014/289349 https://doi.org/10.1155/2014/289349 , [21] Van Den Driessche P, Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Mathematical Biosciences [Internet]. 2002 Oct 1 [cited 2025 Mar 12];180(1–2):29–48. Available from: https://linkinghub.elsevier.com/retrieve/pii/S0025556402001086 https://doi.org/10.1016/S0025-5564(02)00108-6 . The obtained reproduction number (R0hv) shows that in the scenario represented by the model, the disease will ultimately die out. This would mean that fewer than one infection, in both mosquito and human populations, will be generated from a single infected individual. This subsequently reduces incidence over time. The recognition of reducing R0hv to less than 1 has prevention and control connotations: most modern epidemiological practices aim to reduce the reproduction number as the primary focus of infectious disease management. This approach has implications and is critical when aiming for malaria elimination by 2030 [3] World Health Organization. Global Technical Strategy for Malaria 2016–2030: 2021 Update [Internet]. Geneva (Switzerland): World Health Organization; 2021[cited 2025 Mar 12]; 30 p. Available from: https://iris.who.int/bitstream/handle/10665/342995/9789240031357-eng.pdf Download 9789240031357-eng.pdf . As reported elsewhere, there is great potential for malaria as the disease has been eliminated from about 79 countries between 1979 and 2010 [18] Dizon, C., Lysyk, T.J., Couloigner, I. and Cork, S.C. Ecology and Epidemiology of Lyme Disease in Western North America. Zoonotic Diseases [Internet]. 2023 Jan 31;3(1):20-37. Available from: https://www.scienceopen.com/document?vid=a268a629-fd81-43db-997b-cba378686da2 . Disease forecast has shown that beyond the 144th month, February 2027, (figure 3) the number of infected individuals will decline to below 1. This way, the result is helpful in predicting the disease trend in the district which assist in evaluating efforts towards disruption of local transmission, especially so as the district targets zero local malaria transmission by 2030. As has been reported [18] Dizon, C., Lysyk, T.J., Couloigner, I. and Cork, S.C. Ecology and Epidemiology of Lyme Disease in Western North America. Zoonotic Diseases [Internet]. 2023 Jan 31;3(1):20-37. Available from: https://www.scienceopen.com/document?vid=a268a629-fd81-43db-997b-cba378686da2 ., malaria was eliminated from about 79 countries between 1979 and 2010, and according to the report [23] Zimbabwe National Statistics Agency. Masvingo Provincial 2012 Census Report. Harare (Zimbamwe); Zimbabwe National Statistics Agency; 2012 [cited 2025 Mar 15]. 156 p. Available from: https://www.zimstat.co.zw/wp-content/uploads/publications/Population/population/District-Projections/District-Population-Projection-Report-Masvingo.pdf , one district in Zimbabwe had been verified and declared to have eliminated local malaria transmission. However, since the data used in this study was highly fluctuating, possibilities of outbreaks of malaria cannot be ruled out. Consequently, as the district approaches zero local cases caution should be taken to guard against the rebound of the disease. According to research [13] Griffin JT, Bhatt S, Sinka ME, Gething PW, Lynch M, Patouillard E, Shutes E, Newman RD, Alonso P, Cibulskis RE, Ghani AC. Potential for reduction of burden and local elimination of malaria by reducing Plasmodium falciparum malaria transmission: a mathematical modelling study. The Lancet Infectious Diseases [Internet]. 2016 Apr 19 [cited 2025 Mar 12];16(4):465–72. Available from: https://linkinghub.elsevier.com/retrieve/pii/S1473309915004235 https://doi.org/10.1016/S1473-3099(15)00423-5 at low incidence, mosquito bites will also be low, and since immunity is conferred through continued exposure to mosquito bites [12] Selvaraj, P., Wenger, E. A., & Gerardin, J. Seasonality and heterogeneity of malaria transmission determine success of interventions in high-endemic settings: a modeling study. BMC Infectious Diseases [Internet]. 2018 Aug 22 [cited 2025 Mar 12]; 2018(1):413. Available from: https://bmcinfectdis.biomedcentral.com/articles/10.1186/s12879-018-3319-y https://doi.org/10.1186/s12879-018-3319-y , individual immunity will wane, and with an introduction of infected mosquito(es) the disease can bounce back with bouts of cases being experienced. In this study, only a single intervention (LLINs) was modelled as the dominant strategy. However, some other interventions such as case management, behavior change and communication strategies and foci management are also relied on, though they were not modelled in this study. As such further research may be needed which models may incorporate such factors in a bid to formulate a more robust model. Again, in the study aggregated data was used. The age and sex of an individual affects exposure to mosquito bites and subsequent risk of disease. In this study, the mean number of confirmed positive malaria cases were seen to increase with age. This is consistent with observations made by some authors [24] Okell LC, Drakeley CJ, Bousema T, Whitty CJM, Ghani AC. Modelling the Impact of Artemisinin Combination Therapy and Long-Acting Treatments on Malaria Transmission Intensity. PLoS Med [Internet]. 2008 Nov 25 [cited 2025 Mar 12];5(11): e226. Available from: https://dx.plos.org/10.1371/journal.pmed.0050226 https://doi.10.1371/journal.pmed.0050226 , [25] Woolhouse MEJ, Dye C, Etard JF, Smith T, Charlwood JD, Garnett GP, Hagan P, Hii JLK, Ndhlovu PD, Quinnell RJ, Watts CH, Chandiwana SK, Anderson RM. Heterogeneities in the transmission of infectious agents: Implications for the design of control programs. Proc Natl Acad Sci USA [Internet]. 1997 Jan 7 [cited 2025 Mar 12];94(1):338–42. Available from: https://pnas.org/doi/full/10.1073/pnas.94.1.338 https://doi.org/10.1073/pnas.94.1.338 that as one grows older he or she presents a greater surface area available for mosquito bites. As a result, adults seem to have an increased exposure to mosquito bites and risk of suffering from malaria. Again, males contributed more malaria cases compared to their female counterparts. This may be due to the fact that the male population spend greater part of their time outdoors where they get exposed to mosquito bites. However, further modelling studies utilizing disaggregated data by age or sex are suggested. These may yield more reliable evidence as the modelling will take into consideration the variation in disease risk between population categories. While this study provides insights into the district’s malaria transmission dynamics, contextual variations such as socio-economic and cultural factors across districts may affect generalizability of these findings. Future research, however, may consider incorporating diverse districts to enhance robustness and generalizability of the conclusions.Conclusion
This study developed a compartmental model for the transmission of falciparum malaria using ordinary differential equations for both human and mosquito populations. The fundamental presumptions that guided the creation of the model were outlined. The combination impacts of recruitment rates, migration, recovery with temporary immunity and subsequent loss thereof, and infectiousness of the recovered humans – albeit at a lower rate than infectious humans – were demonstrated by the formulation and analysis of the falciparum malaria transmission model.
The DFE point was shown to exist, and to be locally asymptotically stable when R0hv<1. When R0hv<1 the disease will eventually die off.
With a transmission rate of less than one local cases, the model’s numerical simulation demonstrated that, despite the highly variable nature of the transmission dynamics in Masvingo district, the incidence is generally declining. This declining trajectory signifies that the district is on track towards the achievement of WHO 2030 local falciparum malaria elimination target.
Sustaining and building on this trajectory is paramount and requires a multi-faceted approach as well as continued commitment by:
- Promoting behavior change communication to encourage continued widespread distribution and proper usage of long-lasting insecticidal nets (LLINs)
- Ensuring availability and accessibility of rapid diagnostic tests (RDTs) and effective anti-malarial treatment
- Formulating strategies to maintain transmission at low rates thereby preventing resurgence as well as planning for effects of waning immunity at low transmission rates and challenges associated with malaria drug resistance
- Fostering collaborations between research institutions and other stakeholders for better data collection and utilization
- The disease incidence rate is at 4 cases per 1000 PAR
- The district is targeted for local falciparum malaria elimination by the year 2030
- The district is currently using long-lasting insecticidal nets (LLINs), intermittent preventive treatment for pregnant women and infants, case detection, investigation and management
- Deriving the reproduction number for this model provides a quantitative parameter to understand the trajectory for malaria transmission dynamics in the district, and having a reproduction number less than one shows a potential for achieving zero local transmission
- By modelling the human-mosquito interplay underscores the importance of targeting both human and mosquito populations in malaria control as the district strives to achieve zero local malaria transmission
- The model’s prediction that cases could drop to below one case per month by December 2026, given no drug insecticide resistance, gives hope for elimination efforts by providing data-driven insights for continued guided malaria control program planning
- This study also provides a foundation for future research. Any future research can build on this study by incorporating additional factors, such as disaggregated data, to enhance robustness of the model.
Authors´ contributions
Taremba Chirigo conceptualized the study; Taremba Chirigo and Esther Chigidi designed the study; Herbert Tafadzwa Kazonda searched for literature; Taremba Chirigo and Esther Chigidi developed data analysis techniques and analysed the data; Taremba Chirigo drafted the manuscript; Taremba Chirigo, Esther Chigidi and Hebert Tafadzwa Kazonda edited the manuscript. All the authors read and approved the final manuscript.







References
- Osman M, Adu I, Yang C. A Simple SEIR Mathematical Model of Malaria Transmission. ARJOM [Internet]. 2017 Jan 10 [cited 2025 Mar 12];7(3):1–22. Available from: https://journalarjom.com/index.php/ARJOM/article/view/66 https://doi.org/10.9734/ARJOM/2017/37471
- World Health Organization. World Malaria Report 2024: addressing inequity in the global malaria response [Internet]. Geneva (Switzerland): World Health Organization; 2024 Dec 11[cited 2025 Mar 12]; 293 p. Available from: https://www.who.int/teams/global-malaria-programme/reports/world-malaria-report-2024 Download 9789240104440-eng.pdf
- World Health Organization. Global Technical Strategy for Malaria 2016–2030: 2021 Update [Internet]. Geneva (Switzerland): World Health Organization; 2021[cited 2025 Mar 12]; 30 p. Available from: https://iris.who.int/bitstream/handle/10665/342995/9789240031357-eng.pdf
- World Health Organization. Regional data & trends briefing kit: World malaria report 2024. Geneva (Swotzerland): World Health Organization; 2024 Dec 11[cited 2025 Mar 15]. 13 p. Available from: https://cdn.who.int/media/docs/default-source/malaria/world-malaria-reports/world-malaria-report-2024-regional-briefing-kit-eng.pdf?sfvrsn=bceac4ae_9&download=true Download world-malaria-report-2024-regional-briefing-kit-eng.pdf
- Rowe AK. Assessing the Health Impact of Malaria Control Interventions in the MDG/Sustainable Development Goal Era: A New Generation of Impact Evaluations. Am J Trop Med Hyg [Internet]. 2017 Sep 27 [cited 2025 Mar 12];97(3_Suppl):6–8. Available from: https://ajtmh.org/doi/10.4269/ajtmh.17-0509 2017; 97(Suppl 3):6–8. https://doi.org/10.4269/ajtmh.17-0509
- Ministry of Health & Child Care Republic of Zimbabwe. National Health Strategy 2021 – 2025[Internet]. Harare (Zimbabwe): Ministry of Health & Child Care Republic of Zimbabwe; 2021 [cited 2025 Mar 15]. 103 p. Available from: https://www.scribd.com/document/590031144/National-Health-Strategy-for-Zimbabwe-2021-2025 Download National Health Strategy for Zimbabwe[2021_2025]_085222.pdf
- World Health Organization. World malaria report 2018[Internet]. Geneva (Switzerland): World Health Organization; 2018 [cited 2025 Mar 12]. 165 p. Available from: https://iris.who.int/bitstream/handle/10665/275867/9789241565653-eng.pdf?sequence=1 Download 789241565653-eng.pdf
- U.S. President’s Malaria Initiative Zimbabwe Malaria Operational Plan FY 2020 [Internet]. Atlanta (GA): U.S. President’s Malaria Initiative; 2020 [cited 2025 Mar 17]. 133 p. Available from: www.pmi.gov Download ZIMBABWE Malaria Operational Plan FY 2024.pdf
- Ngwa GA, Shu WS. A mathematical model for endemic malaria with variable human and mosquito populations. Mathematical and Computer Modelling [Internet]. 2000 Oct [cited 2025 Mar 12];32(7–8):747–63. Available from: https://linkinghub.elsevier.com/retrieve/pii/S0895717700001692 https://doi.org/10.1016/S0895-7177(00)00169-2
- Walker, P. G. T., Griffin, J. T., Ferguson, N. M., & Ghani, A. C. Estimating the most efficient allocation of interventions to achieve reductions in Plasmodium falciparum malaria burden and transmission in Africa: A modelling study. The Lancet Glob Health [Internet]. 2016 Jul [cited 2025 Mar 12];4(7):e474–e484. Available from: https://www.thelancet.com/journals/langlo/article/PIIS2214-109X(16)30073-0/fulltext https://doi.org/10.1016/S2214-109X(16)30073-0
- Baihaqi, M. A. & Adi-Kusumo, F. Modelling malaria transmission in a population withSEIRp method. Symposium on BioMathematics 2019 ( SYMOMATH 2019) [Internet]. AIP Conf. Proc. 2020; 2264:020002-1 – 020002-12. Bali (Indonesia): AIP Publishing; 2020 Sep 22[cited 2025 Mar 12]; 12 p. Available from: https://pubs.aip.org/aip/acp/article/2264/1/020002/1013132/Modelling-malaria-transmission-in-a-population https://doi.org/10.1063/5.0023508 Download 020002_1_online.pdf
- Selvaraj, P., Wenger, E. A., & Gerardin, J. Seasonality and heterogeneity of malaria transmission determine success of interventions in high-endemic settings: a modeling study. BMC Infectious Diseases [Internet]. 2018 Aug 22 [cited 2025 Mar 12]; 2018(1):413. Available from: https://bmcinfectdis.biomedcentral.com/articles/10.1186/s12879-018-3319-y https://doi.org/10.1186/s12879-018-3319-y
- Griffin JT, Bhatt S, Sinka ME, Gething PW, Lynch M, Patouillard E, Shutes E, Newman RD, Alonso P, Cibulskis RE, Ghani AC. Potential for reduction of burden and local elimination of malaria by reducing Plasmodium falciparum malaria transmission: a mathematical modelling study. The Lancet Infectious Diseases [Internet]. 2016 Apr 19 [cited 2025 Mar 12];16(4):465–72. Available from: https://linkinghub.elsevier.com/retrieve/pii/S1473309915004235 https://doi.org/10.1016/S1473-3099(15)00423-5
- Andolina C, Rek JC, Briggs J, Okoth J, Musiime A, Ramjith J, Teyssier N, Conrad M, Nankabirwa JI, Lanke K, Rodriguez-Barraquer I, Meerstein-Kessel L, Arinaitwe E, Olwoch P, Rosenthal PJ, Kamya MR, Dorsey G, Greenhouse B, Drakeley C, Staedke SG, Bousema T. Sources of persistent malaria transmission in a setting with effective malaria control in eastern Uganda: a longitudinal, observational cohort study. Lancet Infect Dis [Internet]. 2021 Jun 19 [cited 2025 Mar 12];21(11):1568-1578. Available from: https://linkinghub.elsevier.com/retrieve/pii/S1473309921000724 https://doi.org/10.1016/s1473-3099(21)00072-4
- Turkson AJ, Addor JA, Ayiah-Mensah F. The Cox Proportional Hazard Regression Model Vis-à-Vis ITN-Factor Impact on Mortality Due to Malaria. OJS [Internet]. 2021 [cited 2025 Mar 12];11(06):931–62. Available from: https://www.scirp.org/journal/doi.aspx?doi=10.4236/ojs.2021.116055 https://doi.org/10.4236/ojs.2021.116055
- Smith NR, Trauer JM, Gambhir M, Richards JS, Maude RJ, Keith JM, Flegg JA. Agent-based models of malaria transmission: a systematic review. Malar J [Internet]. 2018 Aug 17[cited 2025 Mar 12];17(1):299. Available from: https://malariajournal.biomedcentral.com/articles/10.1186/s12936-018-2442-y https://doi.org/10.1186/s12936-018-2442-y
- Egbom SE, Nduka FO, Nzeako SO. Point prevalence mapping of malaria infection in Rivers State, Nigeria. Tanzania J Hlth Res [Internet]. 2022 Sep 27 [cited 2025 Mar 12];23(4):1–11. Available from: https://www.ajol.info/index.php/thrb/article/view/224077 https://doi.org/10.4314/thrb.v23i4.7
- Dizon, C., Lysyk, T.J., Couloigner, I. and Cork, S.C. Ecology and Epidemiology of Lyme Disease in Western North America. Zoonotic Diseases [Internet]. 2023 Jan 31;3(1):20-37. Available from: https://www.scienceopen.com/document?vid=a268a629-fd81-43db-997b-cba378686da2
- Chitnis N, Hyman JM, Cushing JM. Determining important parameters in the spread of malaria through the sensitivity analysis of a mathematical model. Bull Math Biol [Internet]. 2008 Feb 22 [cited 2025 Mar 12];70(5):1272–96. Available from: http://link.springer.com/10.1007/s11538-008-9299-0 https://doi.org/10.1007/s11538-008-9299-0
- Huo, H., & Qiu, G. Stability of a Mathematical Model of Malaria Transmission with Relapse. Abstract and Applied Analysis [Internet]. 2014[cited 2025 Mar 12]; 2014:1–9. Available from: http://www.hindawi.com/journals/aaa/2014/289349 https://doi.org/10.1155/2014/289349
- Van Den Driessche P, Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Mathematical Biosciences [Internet]. 2002 Oct 1 [cited 2025 Mar 12];180(1–2):29–48. Available from: https://linkinghub.elsevier.com/retrieve/pii/S0025556402001086 https://doi.org/10.1016/S0025-5564(02)00108-6
- Zimbabwe National Statistics Agency. Masvingo Provincial 2012 Census Report. Harare (Zimbamwe); Zimbabwe National Statistics Agency; 2012 [cited 2025 Mar 15]. 156 p. Available from: https://www.zimstat.co.zw/wp-content/uploads/publications/Population/population/District-Projections/District-Population-Projection-Report-Masvingo.pdf
- U.S. President’s Malaria Initiative. ZIMBABWE MALARIA PROFILE [Internet]. Atlanta (GA): U.S. President’s Malaria Initiative; 2024 [cited 2025 Mar 17]. 20 p. Available from: www.pmi.gov
- Okell LC, Drakeley CJ, Bousema T, Whitty CJM, Ghani AC. Modelling the Impact of Artemisinin Combination Therapy and Long-Acting Treatments on Malaria Transmission Intensity. PLoS Med [Internet]. 2008 Nov 25 [cited 2025 Mar 12];5(11): e226. Available from: https://dx.plos.org/10.1371/journal.pmed.0050226 https://doi.10.1371/journal.pmed.0050226
- Woolhouse MEJ, Dye C, Etard JF, Smith T, Charlwood JD, Garnett GP, Hagan P, Hii JLK, Ndhlovu PD, Quinnell RJ, Watts CH, Chandiwana SK, Anderson RM. Heterogeneities in the transmission of infectious agents: Implications for the design of control programs. Proc Natl Acad Sci USA [Internet]. 1997 Jan 7 [cited 2025 Mar 12];94(1):338–42. Available from: https://pnas.org/doi/full/10.1073/pnas.94.1.338 https://doi.org/10.1073/pnas.94.1.338
Menu, Tables and figures
On Google Scholar
Navigate this article
Tables
Table 1: List of parameters for the malaria model and their definitions

Table 2: Descriptive statistics of monthly confirmed (Rapid Diagnostic Test positive) malaria cases disaggregated by age, Masvingo district 2015 -2020

Table 3: Descriptive statistics for malaria occurrence in Masvingo district disaggregated by sex, 2015 - 2020

Table 4: Model parameter values

Figures

Figure 1: Interaction of the different classes of human and mosquito populations. A modified Ngwa and Shu model.


Figure 2: Model fitting to Masvingo district malaria data


Figure 3: Trendline of Malaria Cases in Masvingo district with a forecast as from the 74th month

Keywords
- Deterministic
- Falciparum malaria
- Disease-free equilibrium
- Malaria elimination
- Modelling
- SEIR
- SEI
